Межрелигиозный форум

Информация о пользователе

Привет, Гость! Войдите или зарегистрируйтесь.

Вы здесь » Межрелигиозный форум » Что нового в мире науки? » Пространство

Пространство

Страница:   1 … 6 7 8 9 10 … 34  

Сообщений 211 страница 240 из 1000

211

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76855,Сергей написал(а):

когда ты в гамак плюхаешься, ячейки  гамака растягиваются или сжимаются?
Растягиваются. Так почему у тебя на рисунке ровно наоборот?

Это не мой рисунок. Это рисунок твоих единомышленников. Но ты решил их переплюнуть и представить Землю в виде задницы в гамаке.
Причём гамак это пространство, которое обтекает землю как воздух обтекает ядро Мюнхгаузена в аэротрубе.
Тебя за такую ересь, свои же фундаменталисты  на столбе позора повесят.

Отредактировано Григорий Р (14.01.20 16:03)

0

212

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)

У меня такое , что у Серёжи интернет отключили и он стал думать самостоятельно.

0

213

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76817,Григорий Р написал(а):

В данном случае мистик, из нас двоих это Серёжа.
Я ему говорю за чистую науку, а он несёт мистическую чушь. Чушь со щелью, которая искривлена пространством.

Димачка, ты даже геометрии не знаешь в рамках школьной программы, о какой науке ты можешь говорить? У тебя гиря брошеная на ячейки сетки оказывается сжимает, а не растягивает ячейки.
Димасик, у тебя с головушкой вообще как? Ты хотя бы в школе учился?

0

214

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76862,Сергей написал(а):

У тебя гиря брошеная на ячейки сетки оказывается сжимает, а не растягивает ячейки.

Тебе не надоело своей гирей в кальсонах трясти?
Ты изгибаешь двухмерные кальсоны гравитацией  гири.

Ты вообще думаешь, что делаешь и как это можно сопоставить с Земным шаром, висящиим в трёхмерном киселе пространства?

0

215

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76860,Григорий Р написал(а):

Это не мой рисунок. Это рисунок твоих единомышленников. Но ты решил их переплюнуть и представить Землю в виде задницы в гамаке.

Да это похрен,задница в гамаке или гиря на песке. Ну поставь гирю на песок, ты увидишь как песчинки раздвинутся образуя ямку.Раздвинутся, а не сожмутся.
П

ричём гамак это пространство, которое обтекает землю как воздух обтекает ядро Мюнхгаузена в аэротрубе.
Тебя за такую ересь, свои же фундаменталисты  на столбе позора повесят.

Ты хоть понял в чем лопухнулся, Гриша?

0

216

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76861,Григорий Р написал(а):

У меня такое , что у Серёжи интернет отключили и он стал думать самостоятельно.

А может до тебя наконец дошло, что ахинею несешь?

0

217

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76863,Григорий Р написал(а):

Тебе не надоело своей гирей в кальсонах трясти?
Ты изгибаешь двухмерные кальсоны гравитацией  гири.

Это неконтролируемая  лингводиарея?

Ты вообще думаешь, что делаешь и как это можно сопоставить с Земным шаром, висящиим в трёхмерном киселе пространства?

Повертел пальцем у виска.Это называется визуализацией, Димачка.Объяснение на пальцах.Если ты на этом этапе завис..... :D

0

218

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76864,Сергей написал(а):

Да это похрен,задница в гамаке или гиря на песке. Ну поставь гирю на песок, ты увидишь как песчинки раздвинутся образуя ямку.Раздвинутся, а не сожмутся.

Тогда все пролетающие мимо земли объекты, должны обтекать Землю, как в аэротрубе.
Получается, что внутри Земли пространства нет.

+1

219

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)

Это не то, чтобы просто нобелевка, это памятник на Красной Площади.
Серёжа на ядре.

+1

220

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76867,Григорий Р написал(а):

Тогда все пролетающие мимо земли объекты, должны обтекать Землю, как в аэротрубе.

Они этим и занимается, если  их траектория не заканчивается на поверхности земли.

Получается, что внутри Земли пространства нет.

Даже спрашивать не буду, в результате каких ошибочных умозаключений ты выдал этот перл

0

221

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76869,Григорий Р написал(а):

Это не то, чтобы просто нобелевка, это памятник на Красной Площади.
Серёжа на ядре.

Вот, Гриш, почему самая примитивная геометрия школьного уровня повергла тебя в такой шок? Ведь то, что я тебе говорю,это реально школа.Это не ВУЗ и не какие то секретные знания.Ты это все должен был проходить и понять в седьмом классе. Ну уж по крайней мере, мерность  пространств и объектов ты должен был учить.

0

222

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76876,Сергей написал(а):

Вот, Гриш, почему самая примитивная геометрия школьного уровня повергла тебя в такой шок? Ведь то, что я тебе говорю,это реально школа.Это не ВУЗ и не какие то секретные знания.Ты это все должен был проходить и понять в седьмом классе. Ну уж по крайней мере, мерность  пространств и объектов ты должен был учить.

Я уже устал смеяться.
Твой настольный глобус раздвигает собой пространство? Если прямые линии на нём такие же кривые, как на большой планете.

+1

223

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76878,Григорий Р написал(а):

Я уже устал смеяться.

Тебе бы лучше плакать

Твой настольный глобус раздвигает собой пространство? Если прямые линии на нём такие же кривые, как на большой планете.

Вот сейчас я скажу то, что ты стопроцентно не поймешь.
Если ты положишь глобус на стол, то он постарается раздвинуть поверхность стола и провалиться. Но ему будет мешать реакция опоры.
Если ты запустишь глобус в космос, то таки да, он искривит пространство вокруг себя соответственно своей массе и даже захватит в свою орбиту  частички микропыли .

0

224

  • Автор: Дима1972
  • Ветеран
  • Дима1972
  • Зарегистрирован: 03.09.19
  • Сообщений: 7137
  • Уважение: +1254
  • Позитив: +522
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    21.11.24 23:04
  • Награды:
    31,11#(от Артемиды),26#(от Артемиды),27#(от Артемиды),54#(от Блонди),35#(от Кресчюда),72#(от Сергея и триатмы как ни странно),45#(ot triatma),60#(ot triatma),64#(ot triatma),65#(ot tri),81#(ot tri на вечную память)

Проще говоря, находясь в искривлённом пространстве, нельзя заметить его кривизны. Она видна только из другого пространства, которое само для первого является искривлённым. Глобус шарообразен, но не является искривлённым пространством.

Отредактировано Дима1972 (14.01.20 16:48)

0

225

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76889,Дима1972 написал(а):

Проще говоря, находясь в искривлённом пространстве, нельзя заметить его кривизны. Она видна только из другого пространства, которое само для первого является искривлённым. )

Ну как то так ,да

Глобус шарообразен, но не является искривлённым пространством.

А внутри?

0

226

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76886,Сергей написал(а):

Если ты положишь глобус на стол, то он постарается раздвинуть поверхность стола и провалиться. Но ему будет мешать реакция опоры.
Если ты запустишь глобус в космос, то таки да, он искривит пространство вокруг себя соответственно своей массе и даже захватит в свою орбиту  частички микропыли .

Это касается только глобуса или любых предметов?

0

227

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76892,Сергей написал(а):

А внутри?

А внутри глобуса, по твоей теории нет пространства. Или оно есть, но изрядно растянуто.
Таким образом,  тараканы, попавшие внуть глобуса кажутся в несколько раз больше и преодолевают расстояния в несколько раз быстрее.

Памятник рядом с Гагариным. Не меньше.

+1

228

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76893,Григорий Р написал(а):

Это касается только глобуса или любых предметов?

Любых предметов. На любой предмет лежащий на плоскости в поле гравитации, действует реакция опоры. И любой предмет запущенный в космос, будет искривлять вокруг себя пространство соответственно своей массе

0

229

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76896,Сергей написал(а):

Любых предметов. На любой предмет лежащий на плоскости в поле гравитации, действует реакция опоры. И любой предмет запущенный в космос, будет искривлять вокруг себя пространство соответственно своей массе

Слава Богу. А то я подумал у тебя фиксация на глобус.

+1

230

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76895,Григорий Р написал(а):

А внутри глобуса, по твоей теории нет пространства.

С чего бы это?

Или оно есть, но изрядно растянуто.
Таким образом,  тараканы, попавшие внуть глобуса кажутся в несколько раз больше и преодолевают расстояния в несколько раз быстрее.

Памятник рядом с Гагариным. Не меньше.

М...да. Печально это все. Поциэнт взялся городить ахинею

0

231

  • Автор: Блонди
  • 🕉
  • Блонди
  • Зарегистрирован: 15.01.19
  • Сообщений: 12536
  • Уважение: +5669
  • Позитив: +10751
  • Пол: Женский
  • Возраст: 40 [1984-04-05]
  • Провел на форуме:
    2 месяца 20 дней
  • Последний визит:
    20.11.24 06:54
  • Награды:
    31,16#(от АЯ),11#(от Артемиды),29#(от Артемиды),12#(от ~Татьяны~ и Григория Р),1#(от Григория Р),14#(от Григория Р),46#(от Сергея),7#(от Триатмы),8#(от Триатмы),19#(от Триатмы),72#(от Сергея),16#(от Enigma),46#(от conformist),85#(от Enigma),98#(от Enigma),12#(от Enigma),29#(от Стефании),7#(от Бастет),14#(от conformist),114#(от Lisa),16#(от Конформиста)

:rofl:

0

232

  • Автор: Блонди
  • 🕉
  • Блонди
  • Зарегистрирован: 15.01.19
  • Сообщений: 12536
  • Уважение: +5669
  • Позитив: +10751
  • Пол: Женский
  • Возраст: 40 [1984-04-05]
  • Провел на форуме:
    2 месяца 20 дней
  • Последний визит:
    20.11.24 06:54
  • Награды:
    31,16#(от АЯ),11#(от Артемиды),29#(от Артемиды),12#(от ~Татьяны~ и Григория Р),1#(от Григория Р),14#(от Григория Р),46#(от Сергея),7#(от Триатмы),8#(от Триатмы),19#(от Триатмы),72#(от Сергея),16#(от Enigma),46#(от conformist),85#(от Enigma),98#(от Enigma),12#(от Enigma),29#(от Стефании),7#(от Бастет),14#(от conformist),114#(от Lisa),16#(от Конформиста)
#p76767,Сергей написал(а):
#p76744,Григорий Р написал(а):

Да ты Архимед от природы!
Возьми глобус и нитку с иглой. Найди две любые точки.

Самое кратайшее растояние между точками - прямая. Между любыми.
Протни шилом глобус и проверь.

Твою ж мать. Ведь школьная же программа же.

Если смотреть на траекторию полета на дисплее в салоне или дома на компьютере, то она выглядит не прямой, а дугообразной, выгнутой в сторону ближайшего полюса (северного в северном полушарии, южного в южном). На самом же деле самолет на протяжении практически всего маршрута (и чем он длиннее, тем это справедливее) старается лететь именно по прямой. Просто дисплеи плоские, а Земля круглая, и проекция объемной карты на плоскую видоизменяет ее пропорции: чем ближе к полюсам, тем более изогнутой окажется «дуга». Проверить это очень просто: возьмите глобус и натяните по его поверхности нитку между двумя городами. Это и будет кратчайший маршрут. Если же теперь перенести линию нитки на бумагу, у вас получится дуга.
https://www.frequentflyers.ru/wp-content/uploads/2014/04/%D0%A1%D0%BA%D1%80%D0%B8%D0%BD%D1%88%D0%BE%D1%82-2014-04-02-23.59.01-e1396468874130.png
https://www.frequentflyers.ru/2014/04/0 … uting_faq/

При переносе 3-х мерной траектории на 2-х мерную систему координат только ракурс решает, на сколько линия будет прямой или кривой :D дубинушка

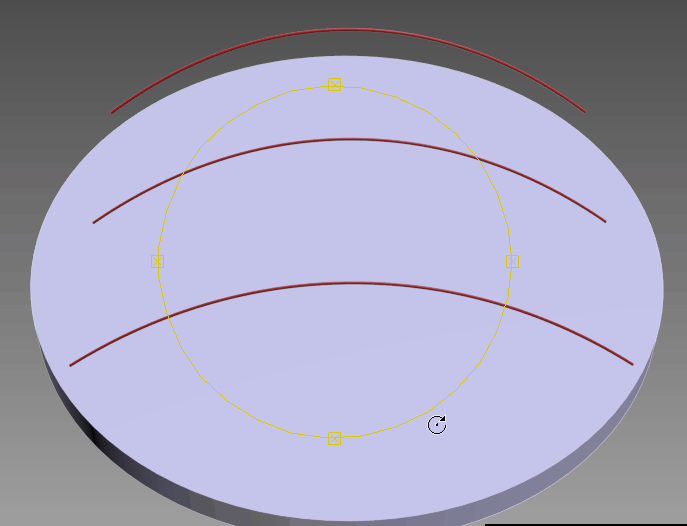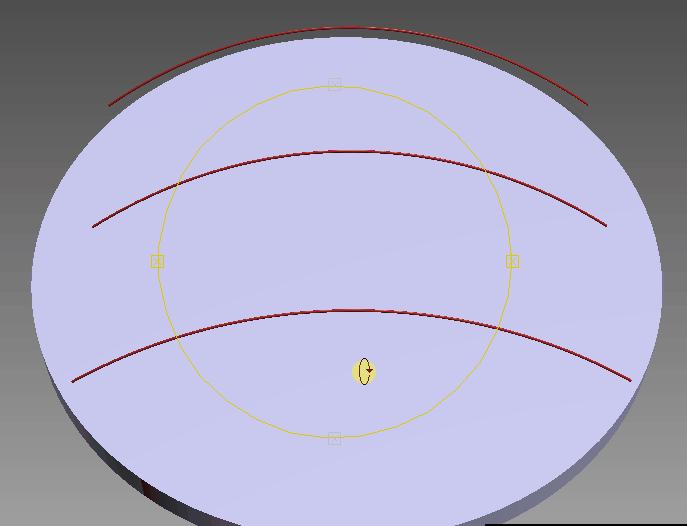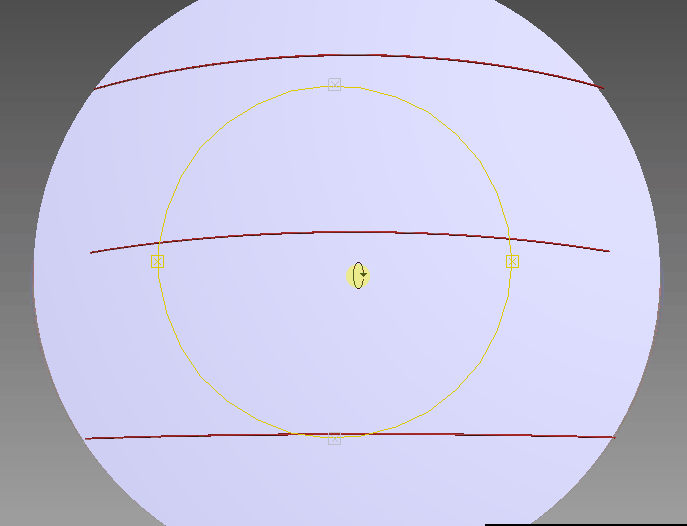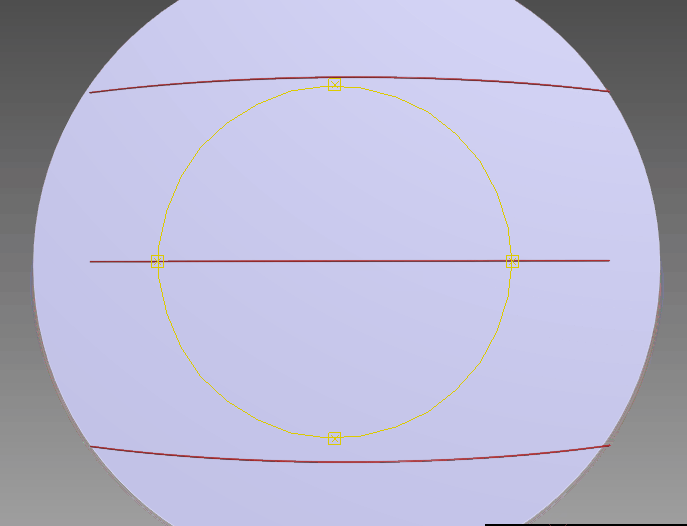
http://images.vfl.ru/ii/1578990811/a03eaac8/29196164.gif

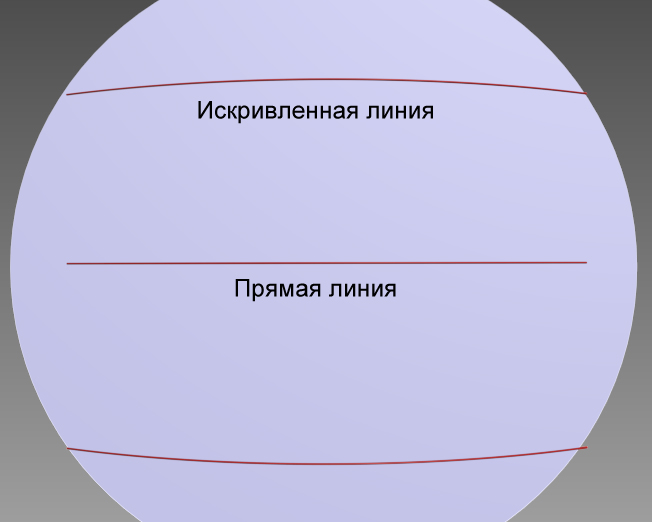
http://images.vfl.ru/ii/1578990727/f05a75f2/29196151.jpg

Отредактировано Блонди (14.01.20 17:52)

0

233

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p76918,Блонди написал(а):
#p76767,Сергей написал(а):
#p76744,Григорий Р написал(а):

Да ты Архимед от природы!
Возьми глобус и нитку с иглой. Найди две любые точки.

Самое кратайшее растояние между точками - прямая. Между любыми.
Протни шилом глобус и проверь.

Твою ж мать. Ведь школьная же программа же.

Если смотреть на траекторию полета на дисплее в салоне или дома на компьютере, то она выглядит не прямой, а дугообразной, выгнутой в сторону ближайшего полюса (северного в северном полушарии, южного в южном). На самом же деле самолет на протяжении практически всего маршрута (и чем он длиннее, тем это справедливее) старается лететь именно по прямой. Просто дисплеи плоские, а Земля круглая, и проекция объемной карты на плоскую видоизменяет ее пропорции: чем ближе к полюсам, тем более изогнутой окажется «дуга». Проверить это очень просто: возьмите глобус и натяните по его поверхности нитку между двумя городами. Это и будет кратчайший маршрут. Если же теперь перенести линию нитки на бумагу, у вас получится дуга.
https://www.frequentflyers.ru/wp-content/uploads/2014/04/%D0%A1%D0%BA%D1%80%D0%B8%D0%BD%D1%88%D0%BE%D1%82-2014-04-02-23.59.01-e1396468874130.png
https://www.frequentflyers.ru/2014/04/0 … uting_faq/

При переносе 3-х мерной траектории на 2-х мерную систему координат только ракурс решает, на сколько линия будет прямой или кривой :D дубинушка

http://images.vfl.ru/ii/1578990811/a03eaac8/29196164.gif

http://images.vfl.ru/ii/1578990727/f05a75f2/29196151.jpg

Это страшное дело. Девочка даже не задумывается, что все меридианы сходятся в две точки. И с какого ракурса не взгляни на две нижних параллели на плоской карте, они так и останутся дугами
Ну хорошо, вот перенос с трехмерной модели на двухмерную
https://www.frequentflyers.ru/wp-content/uploads/2014/04/%D0%A1%D0%BA%D1%80%D0%B8%D0%BD%D1%88%D0%BE%D1%82-2014-04-02-23.59.01-e1396468874130.png
С какого ракурса ты будешь смотреть на плоскую карту, что бы маршрут стал прямым?.

0

234

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)

http://www.comciencia.br/wp-content/uploads/2019/05/idel_01.jpg
https://i.imgur.com/rsFDAI8m.gif
Последняя картинка анимирована.Жми

Отредактировано Сергей (14.01.20 18:22)

0

235

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p76923,Сергей написал(а):

Это страшное дело. Девочка даже не задумывается, что все меридианы сходятся в две точки. И с какого ракурса не взгляни на две нижних параллели на плоской карте, они так и останутся дугами
Ну хорошо, вот перенос с трехмерной модели на двухмерную

С какого ракурса ты будешь смотреть на плоскую карту, что бы маршрут стал прямым?.

Серёжа, а ты точно не блондинка?  С полётного ракурса! С какого же ещё.

А мы смотрим с экваторной развёртки.

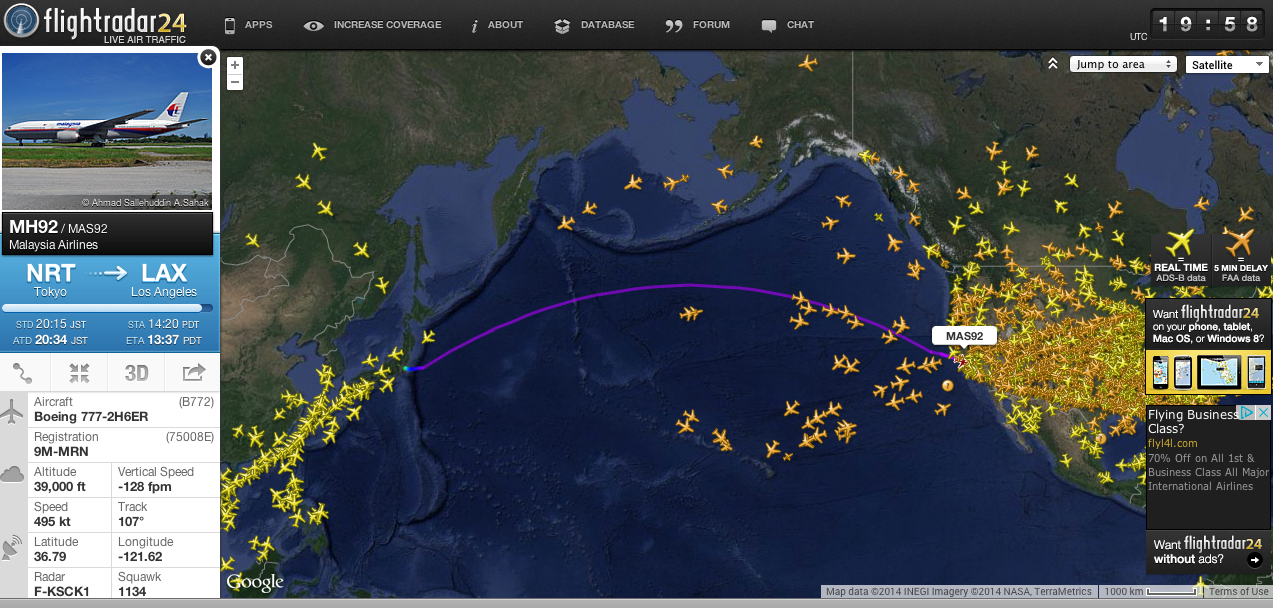
Посмотри сюда. Самолёт Токио-Лос-Анджелес летит по короткому участку той же траектории, что и жёлтое кольцо спутника. Если развернуть карту глобуса взяв за ось экватор, то проекция траектории будет синусоидной.

А если ты будешь смотреть с ракурса траектории, как на этой картинке, то траектория будет ровнейшей линией на развёртке. А экватор на развёртке будет синусоидой.

Просто невозможно выбирать ракурсы для каждого самолёта.

https://www.stihi.ru/pics/2018/01/17/11890.jpg

Ты никогда не видел траектории ровно летящих спутников в развёртке относительно экватора? Если сделать развёртку относительно орбиты, то синусоидой будет уже экватор.

http://cdn01.ru/files/users/images/2e/6c/2e6cce9e8e5222df9204d6f00a79ae9a.png

Как раз в правом верхнем углу, жёлтым цветом, траектория прямого соединения точек Токио - Лос Анджелес.
Прямее некуда! Это же спутник.

Тебя никогда не возьмут в космонавты, Серёжа.

А так будет выглядеть ракурс, если мы полетим дальше по этой же орбите в Сидней.

http://cdn01.ru/files/users/images/2c/ed/2ceda32ccd03201297356ce267232d85.jpg

А если ты измеряешь эти дуги по линейке на кривой развёртке, то посмотри на развёртку береговой линии Антарктиды. Ты тоже думаешь, что это самая длинная береговая линия в мире?

Отредактировано Григорий Р (14.01.20 19:39)

0

236

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p76744,Григорий Р написал(а):

Да ты Архимед от природы!
Возьми глобус и нитку с иглой. Найди две любые точки.

Самое кратайшее растояние между точками - прямая. Между любыми.
Протни шилом глобус и проверь.

Гриш, приложи холодный компресс ко-лбу и прочти внимательно: тебе писали об особенностях одного пространства, переложимых на другое пространство, с меньшей мерностью. Так вот относительно двухмерного, в трехмерном пространстве кратчайшее расстояние - это дуга. А не дуга в принципе, как абстрактное понятие. Отсюда предложение проткнуть глобус - это твои шизики, поскольку это действие по третьей координате, которая в двухмерном пространстве осус-сует.
Ты просил показать искривление пространства, насколько понимаю? Так вот тебе и показали это самое на примере движения по трехмерному для двух координат. Чего тупишь-то?

0

237

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p76947,Дима1972 написал(а):

Нет, начерталка, это конкретная дисциплина, которую проходят в вузе. Там надо достраивать незаконченные фигуры. Есть люди, для которых это вообще не проблема, а есть совершенно неспособные к этому. Возьмите учебник начертательной геометрии, кажется фридмана, сами поймёте, к какой категории относитесь.

Хотя, по вопросу отсутствия прямой связи с наличием интеллекта, соглашусь. Многие людит мыслят словами, а не образами, им начерталка трудна.

Оперирование в пространстве не имеет отношения к разрешению какой-либо проблемы, поскольку не подразумевает ни анализа, ни синтеза, выполняясь простым соответствием заведомо данным свойствам. Хороший пример - движения рук. Механически - сложнейший процесс, включающий сотни, если не тысячи действующих составляющих: согласованное сокращение мышц и точная степень силы, ими вырабатываемая, умноженная на доли секунды представляет огромную сложность для робототехники даже сегодня. А мозг легко справляется с этим, просто управляя рукой, как единым целым - дальше же в игру вступают чисто механические закономерности, положенные в особенность конструкции, автоматически предопределяя то или иное действие.
Так же и здесь: мышление в рамках дисциплины никакого отношения не имеет к качеству мышления в общем и прямо никак не соотносится с производимыми операциями.

Что же на счет образного мышления, то оно является наиболее примитивным и доминирует у детей, если мне не изменяет память, до четырех лет. Позже на первый план выходит абстрактное мышление, но, видимо, не все этой участью обременены...

0

238

  • Автор: Владимир
  • Ветеран
  • Владимир
  • Зарегистрирован: 30.07.19
  • Сообщений: 3899
  • Уважение: +374
  • Позитив: +200
  • Провел на форуме:
    22 дня 7 часов
  • Последний визит:
    16.03.20 15:14
#p76860,Григорий Р написал(а):

Это не мой рисунок. Это рисунок твоих единомышленников. Но ты решил их переплюнуть и представить Землю в виде задницы в гамаке.
Причём гамак это пространство, которое обтекает землю как воздух обтекает ядро Мюнхгаузена в аэротрубе.
Тебя за такую ересь, свои же фундаменталисты  на столбе позора повесят.

Отредактировано Григорий Р (Сегодня 08:03)

Григорий, вам не надоело в дубовый лоб каблуком бить? Ведь можно взять абсолютную прямую (нитку) и приложить ее к любому мередиану на глобусе. Нитка от искревления земли ни капли не увеличится или не уменьшится. Так измеряется прямая длинна. Но если вы зафиксируете нитку в любом положении и потом попробуете изменить ее положение, произойдет либо напряжение, либо ослабление. Космические искривления предполагают изменения. Вопрос: Что изменяется?

Подпись автора

Ты уже знаешь, зачем живешь?

0

239

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p76918,Блонди написал(а):

При переносе 3-х мерной траектории на 2-х мерную систему координат только ракурс  решает, на сколько линия будет прямой или кривой :D дубинушка

Стесняюсь спросить, а каким местом Вы компенсируете движение по третьей координате в двухмерном пространстве? Или у Вас время и скорость тоже от ракурса зависят?:D

+1

240

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p76968,Дима1972 написал(а):

Так можно сказать о решении абсолютно любых задач.

Вот видишь, как получается. Используемая форма совсем не при чем, важна лишь степень эффективной продуктивности, что и определяет качество интеллекта. Как только мы касаемся способов осуществления - будь то слово, образ или цифра, то немедленно попадаем на уровень дитеныша о четырех неполных годах. Способ ничего не показывает.

#p76968,Дима1972 написал(а):

Задачи начерталки ничем не отличаются от задач иных наук. И они являются абстрактным мышлением в чистом виде, вместо предметов сознание подставляет образы, содержащие исключительно важные для задачи признаки реальных вещей.

Да, конечно. Только речь шла не о задачах, а об операциях, реализуемых конкретным способом. На этом ты и провалился, ошибочно поставив между ними знак равенства.

0

Страница:   1 … 6 7 8 9 10 … 34  

Вы здесь » Межрелигиозный форум » Что нового в мире науки? » Пространство