Межрелигиозный форум

Информация о пользователе

Привет, Гость! Войдите или зарегистрируйтесь.

Вы здесь » Межрелигиозный форум » Что нового в мире науки? » Пространство

Пространство

Страница:   1 … 21 22 23 24 25 … 34  

Сообщений 661 страница 690 из 1000

661

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p80001,Сергей написал(а):

Гриша, она не равна нулю, просто векторы уравновешиваются

А теперь попробуй объяснить ему разДниццу.:D Рискни! 'Сделай "Дью"!'

Если он поверхность и плоскость не умеет соотнести, я теряюсь в представлении, сколько страниц на это понадобится...

#p80001,Сергей написал(а):

Гриша, тупость несусветная, услышь мой месседж! Объект гнет внешнее пространство, а не пространство объект

Сотый раз писано - и все не в прок. Бронелобый мамонт по кличке Гриша так и неувидел море.
Какая жаль.

0

662

  • Автор: Дима1972
  • Ветеран
  • Дима1972
  • Зарегистрирован: 03.09.19
  • Сообщений: 7137
  • Уважение: +1254
  • Позитив: +522
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    21.11.24 23:04
  • Награды:
    31,11#(от Артемиды),26#(от Артемиды),27#(от Артемиды),54#(от Блонди),35#(от Кресчюда),72#(от Сергея и триатмы как ни странно),45#(ot triatma),60#(ot triatma),64#(ot triatma),65#(ot tri),81#(ot tri на вечную память)
#p80017,Григорий Р написал(а):

Шарик, ты балбес.

Кратчайший маршрут из любой точки А земного шара, в иную точку В того же шара лежит строго в прямой плоскости, проходяшей  через центр земного шара.
Эта плоскость ПРЯМАЯ.
Значит на эту плоскость можно посмотреть под таким углом, что она превратится в прямую линию со всем содержимым.
Но ты снова ничего не понял.

Мне кажется, мы достигли того знаменательного момента, когда уже все участники разговора поняли, что экватор может быть проведён через две любые точки шара. В начале разговора это знание было многим недоступно.

+1

663

  • Автор: Блонди
  • 🕉
  • Блонди
  • Зарегистрирован: 15.01.19
  • Сообщений: 12536
  • Уважение: +5669
  • Позитив: +10751
  • Пол: Женский
  • Возраст: 40 [1984-04-05]
  • Провел на форуме:
    2 месяца 20 дней
  • Последний визит:
    20.11.24 06:54
  • Награды:
    31,16#(от АЯ),11#(от Артемиды),29#(от Артемиды),12#(от ~Татьяны~ и Григория Р),1#(от Григория Р),14#(от Григория Р),46#(от Сергея),7#(от Триатмы),8#(от Триатмы),19#(от Триатмы),72#(от Сергея),16#(от Enigma),46#(от conformist),85#(от Enigma),98#(от Enigma),12#(от Enigma),29#(от Стефании),7#(от Бастет),14#(от conformist),114#(от Lisa),16#(от Конформиста)

Открываешь сайт - https://www.flightradar24.com/UAE225/239b52bc

И смотришь на прямолинейные траектории воочию.

https://images.vfl.ru/ii/1579686098/d9267d84/29283543.jpg

https://images.vfl.ru/ii/1579686098/c49bfdeb/29283544.jpg

http://images.vfl.ru/ii/1579686592/7fd8606f/29283675.jpg

Отредактировано Блонди (22.01.20 12:50)

0

664

  • Автор: Дима1972
  • Ветеран
  • Дима1972
  • Зарегистрирован: 03.09.19
  • Сообщений: 7137
  • Уважение: +1254
  • Позитив: +522
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    21.11.24 23:04
  • Награды:
    31,11#(от Артемиды),26#(от Артемиды),27#(от Артемиды),54#(от Блонди),35#(от Кресчюда),72#(от Сергея и триатмы как ни странно),45#(ot triatma),60#(ot triatma),64#(ot triatma),65#(ot tri),81#(ot tri на вечную память)
#p80054,Блонди написал(а):

Открываешь сайт - https://www.flightradar24.com/UAE225/239b52bc

И смотришь на прямолинейные траектории воочию.

Более того, если карту увеличить и сдвинуть её центр, то линии будут искривляться. Это связано неис гравитацией, а с искажением проекции меркатора.

0

665

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80051,Ystyrgar написал(а):

А теперь попробуй объяснить ему разДниццу. Рискни! 'Сделай "Дью"!'

Если он поверхность и плоскость не умеет соотнести, я теряюсь в представлении, сколько страниц на это понадобится...

Сотый раз писано - и все не в прок. Бронелобый мамонт по кличке Гриша так и неувидел море.
Какая жаль.

Я их уже боюсь. Ну ладно, если один  Вова-🌻. Но этих чудиков уже трое

0

666

  • Автор: Дима1972
  • Ветеран
  • Дима1972
  • Зарегистрирован: 03.09.19
  • Сообщений: 7137
  • Уважение: +1254
  • Позитив: +522
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    21.11.24 23:04
  • Награды:
    31,11#(от Артемиды),26#(от Артемиды),27#(от Артемиды),54#(от Блонди),35#(от Кресчюда),72#(от Сергея и триатмы как ни странно),45#(ot triatma),60#(ot triatma),64#(ot triatma),65#(ot tri),81#(ot tri на вечную память)

https://media.ykt.ru/upload/photo/2018/11/20/normal/f778a088-aedc-490e-b6a9-171433e0a61a.png

0

667

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80043,Блонди написал(а):

Серёжа, а почему здесь траектории полета самолета на плоской карте нарисованы местами ровные?

https://www.nn.ru/news/more/polet_norma … /65294391/

Судя по всему,это глиссады и  зона ожидания для посадки :rofl:

0

668

  • Автор: Дима1972
  • Ветеран
  • Дима1972
  • Зарегистрирован: 03.09.19
  • Сообщений: 7137
  • Уважение: +1254
  • Позитив: +522
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    21.11.24 23:04
  • Награды:
    31,11#(от Артемиды),26#(от Артемиды),27#(от Артемиды),54#(от Блонди),35#(от Кресчюда),72#(от Сергея и триатмы как ни странно),45#(ot triatma),60#(ot triatma),64#(ot triatma),65#(ot tri),81#(ot tri на вечную память)
#p80065,Сергей написал(а):

Я их уже боюсь. Ну ладно, если один  Вова-🌻. Но этих чудиков уже трое

Алло, дорогая, только что по радио передали, что один псих едет по встречке. Будь осторожнее!
— Один? Да их тут , млядь, тысячи! anekdotov.net

+1

669

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80047,Дима1972 написал(а):

Вы с сергеем просто услышали гдето красивый термин искривление пространства, и занизили его смысл до своего уровня понимания.

Ну да, ну да. Как же по другому то :D

0

670

  • Автор: Блонди
  • 🕉
  • Блонди
  • Зарегистрирован: 15.01.19
  • Сообщений: 12536
  • Уважение: +5669
  • Позитив: +10751
  • Пол: Женский
  • Возраст: 40 [1984-04-05]
  • Провел на форуме:
    2 месяца 20 дней
  • Последний визит:
    20.11.24 06:54
  • Награды:
    31,16#(от АЯ),11#(от Артемиды),29#(от Артемиды),12#(от ~Татьяны~ и Григория Р),1#(от Григория Р),14#(от Григория Р),46#(от Сергея),7#(от Триатмы),8#(от Триатмы),19#(от Триатмы),72#(от Сергея),16#(от Enigma),46#(от conformist),85#(от Enigma),98#(от Enigma),12#(от Enigma),29#(от Стефании),7#(от Бастет),14#(от conformist),114#(от Lisa),16#(от Конформиста)
#p80069,Сергей написал(а):
#p80043,Блонди написал(а):

Серёжа, а почему здесь траектории полета самолета на плоской карте нарисованы местами ровные?

https://www.nn.ru/news/more/polet_norma … /65294391/

Судя по всему,это глиссады и  зона ожидания для посадки :rofl:

Дубинушка, это та же программа, что Вы использовали уже.
Flightradar.

#p76767,Сергей написал(а):
#p76744,Григорий Р написал(а):

Да ты Архимед от природы!
Возьми глобус и нитку с иглой. Найди две любые точки.

Самое кратайшее растояние между точками - прямая. Между любыми.
Протни шилом глобус и проверь.

Твою ж мать. Ведь школьная же программа же.

Если смотреть на траекторию полета на дисплее в салоне или дома на компьютере, то она выглядит не прямой, а дугообразной, выгнутой в сторону ближайшего полюса (северного в северном полушарии, южного в южном). На самом же деле самолет на протяжении практически всего маршрута (и чем он длиннее, тем это справедливее) старается лететь именно по прямой. Просто дисплеи плоские, а Земля круглая, и проекция объемной карты на плоскую видоизменяет ее пропорции: чем ближе к полюсам, тем более изогнутой окажется «дуга». Проверить это очень просто: возьмите глобус и натяните по его поверхности нитку между двумя городами. Это и будет кратчайший маршрут. Если же теперь перенести линию нитки на бумагу, у вас получится дуга.
https://www.frequentflyers.ru/wp-content/uploads/2014/04/%D0%A1%D0%BA%D1%80%D0%B8%D0%BD%D1%88%D0%BE%D1%82-2014-04-02-23.59.01-e1396468874130.png
https://www.frequentflyers.ru/2014/04/0 … uting_faq/

Наравне с дугообразными траекториями есть еще и прямые.
Почему?

https://i.imgur.com/273xExIl.jpg

Отредактировано Блонди (22.01.20 13:46)

0

671

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p80027,Сергей написал(а):

по баранизму своему начал придумывать условия и приплел экватор. Хотя и там при переносе на плоскую карту, маршрут получается дугой.

На плоской проекции это прямая!
Отклонение от экватора даёт кривизну. Чем дальше тем круче из -за искажений проекции.

И это никак не доказывает искривление пространства.

0

672

  • Автор: Блонди
  • 🕉
  • Блонди
  • Зарегистрирован: 15.01.19
  • Сообщений: 12536
  • Уважение: +5669
  • Позитив: +10751
  • Пол: Женский
  • Возраст: 40 [1984-04-05]
  • Провел на форуме:
    2 месяца 20 дней
  • Последний визит:
    20.11.24 06:54
  • Награды:
    31,16#(от АЯ),11#(от Артемиды),29#(от Артемиды),12#(от ~Татьяны~ и Григория Р),1#(от Григория Р),14#(от Григория Р),46#(от Сергея),7#(от Триатмы),8#(от Триатмы),19#(от Триатмы),72#(от Сергея),16#(от Enigma),46#(от conformist),85#(от Enigma),98#(от Enigma),12#(от Enigma),29#(от Стефании),7#(от Бастет),14#(от conformist),114#(от Lisa),16#(от Конформиста)
#p80082,Григорий Р написал(а):
#p80027,Сергей написал(а):

по баранизму своему начал придумывать условия и приплел экватор. Хотя и там при переносе на плоскую карту, маршрут получается дугой.

На плоской проекции это прямая!
Отклонение от экватора даёт кривизну. Чем дальше тем круче из -за искажений проекции.

И это никак не доказывает искривление пространства.

Гриша, ты почитай, что по ссылке написано, которую Серёженька нам скидывал в доказательство искривления пространства - https://www.frequentflyers.ru/2014/04/0 … uting_faq/

Что называется - Серёжа смотрит в книгу и видит фигу.

0

673

  • Автор: Блонди
  • 🕉
  • Блонди
  • Зарегистрирован: 15.01.19
  • Сообщений: 12536
  • Уважение: +5669
  • Позитив: +10751
  • Пол: Женский
  • Возраст: 40 [1984-04-05]
  • Провел на форуме:
    2 месяца 20 дней
  • Последний визит:
    20.11.24 06:54
  • Награды:
    31,16#(от АЯ),11#(от Артемиды),29#(от Артемиды),12#(от ~Татьяны~ и Григория Р),1#(от Григория Р),14#(от Григория Р),46#(от Сергея),7#(от Триатмы),8#(от Триатмы),19#(от Триатмы),72#(от Сергея),16#(от Enigma),46#(от conformist),85#(от Enigma),98#(от Enigma),12#(от Enigma),29#(от Стефании),7#(от Бастет),14#(от conformist),114#(от Lisa),16#(от Конформиста)

"Просто дисплеи плоские, а Земля круглая, и проекция объемной карты на плоскую видоизменяет ее пропорции: чем ближе к полюсам, тем более изогнутой окажется «дуга»."

0

674

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p80053,Дима1972 написал(а):

Мне кажется, мы достигли того знаменательного момента, когда уже все участники разговора поняли, что экватор может быть проведён через две любые точки шара. В начале разговора это знание было многим недоступно.

Да, Сереженька по глупости начал пихать эти картинки, подсмотренные в Шереметьего из-за плеча дипломированных диспетчеров. Пока со шлангом бегал и воду включал.

Сейчас апельсины суёт.  Если всё это задумывалось, чтобы показать нам, что земля круглая, и путешественник делает круг по поверхности, то достаточно апельсина.
Он нам хотел какое-то свое открытие показать.
Но вовремя спрыгнул.
Ну, как вовремя. На тысячной странице где-то.

Отредактировано Григорий Р (22.01.20 14:11)

0

675

  • Автор: Кресчюд
  • Ветеран
  • Зарегистрирован: 22.07.19
  • Сообщений: 4224
  • Уважение: +272
  • Позитив: +23
  • Пол: Мужской
  • Возраст: 47 [1977-09-08]
  • Провел на форуме:
    1 месяц 15 дней
  • Последний визит:
    15.10.24 19:48
  • Награды:
    31,31#(от Блонди),36#(от Блонди),49#(от Триатмы),59#(от Блонди),21#(от Григорий Р),9#(от Григорий Р),129#(от Артмеиды),109#(от Lisa),82#(от Бастет),61#(от Бастет)

Пространство как людской научный термин это ни что то или его отсутствие.

А всего лишь определенная координата измеряемая  как кому угодно.

Это может быть как твердый объект так и абсолютная пустота.

Потому что это не имеет значение.

Это может быть часть чего то или много чего.

Пространство это обозначение определенного места.

В двух измерениях или трёх, как кому хочется.

Кривое или прямое или частично кривое и частично прямое.

И если мы его обозначили, то ничего его не может изменить.

Координаты не могут меняться.

Чтобы там не произошло в этих координатах.

Подпись автора

Всё ни так как кажется.
Спроси меня и я не отвечу тебе. Но расскажу новое и чудное, то что сам не знаю.

0

676

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p80015,Григорий Р написал(а):

Ну, ты понял как ты облажался?

Давай поглядим внимательнее...

#p80015,Григорий Р написал(а):

Кратчайший путь самолёта из любой точки шара в любую точку лежит в плоскости, которая проходит через центр шара. Читай экватор.

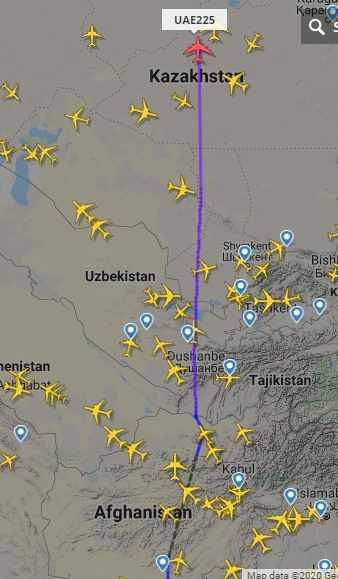
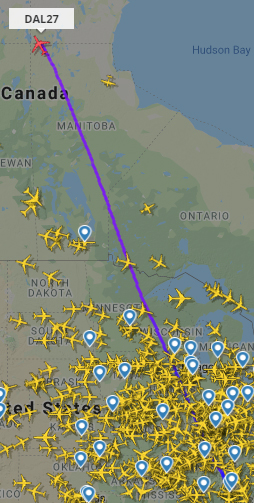
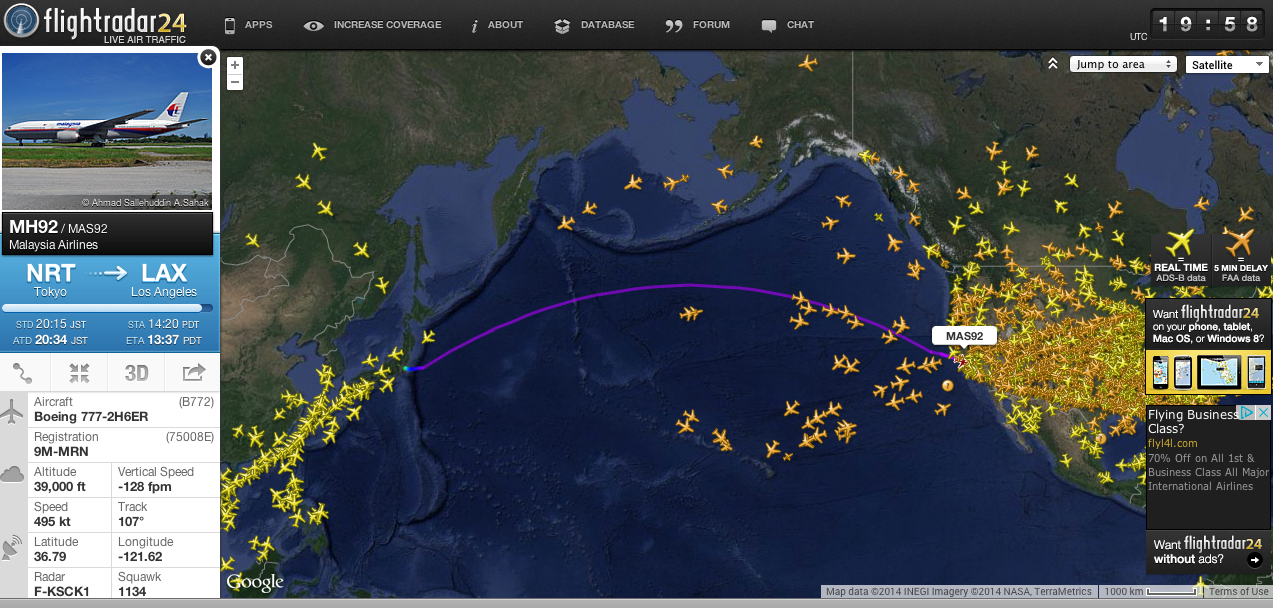
Погоди с экватором, у нас траектория на поверхности сферы. "Урони" ее на плоскость. Чего получишь? Прямую? Или дугу?
Если смотреть сверху, на ту же траекторию, будет прямая. Но эта прямая будет искажением реальной траектории, как по времени, так и по  длине. Выходит, снова дуга, чтобы компенсировать перемещение по третьей координате. Но все это касается фактической кривизны пути только по одной из двух осей ("х" или "у" - без разницы). Кратчайшее расстояние здесь уже - дуга, если смотреть из трехмерного пространства, в проекции траектории на двухмерное. И ослу понятно, что для двухмерного кратчайшим останется путь по прямой - из А в Б. Но мы то говорим об ИСКРИВЛЕНИИ, а оно всегда относительно чего-нибудь. В данном случае - трехмерного пространства.
Это все пока касается искривлением только абстрактного линейного пути, у которого "ширина" (вторая координата) отсутствует, а не плоскости, в которой он лежит. Про плоскость будет ниже.

#p80015,Григорий Р написал(а):

Так вот, экватор же у тебя прямой на экваториальной развёртке.

Экватор, наконец.
Гриня, движение по экватору, это не отрезок АБ. Это окружность АА, которая, естественно, замкнута сама на себя - точно также, как "дырка" (окружность) твоего цилиндра. А что это значит? А это значит, что ее искривление полностью скомпенсированы, образуя прилежащую плоскость. Незамкнутая линия такой компенсации не имеет, потому и образует дугу в прилежащей к ней плоскости НА СФЕРЕ.
В полной развертке у тебя любая параллель будет отнюдь не прямой, а явит собой окружность, как и экватор. Прямой он лишь на схематическом отображении. Как, например, в сегментированной карте, где плоскость поделена на равные части. Но это уже приспособление трехмерного пространства под одномерное пространство - под координату самого экватора.

0

677

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p80001,Сергей написал(а):

Гриша, тупость несусветная, услышь мой месседж! Объект гнет внешнее пространство, а не пространство объект

Глупец, гравитация действует во всей плотности Земли. Не только во внешнем пространстве.
В очень глубокой шахте тоже. Вплоть до центра.
А ведь ты говлрил, что гравитация есть следствие искривления пространства.
Значит пространство кривое  и в толще шара.
Ты же не будешь стоять на том, что пространства там нет, оно вытеснено веществом.

0

678

  • Автор: Кресчюд
  • Ветеран
  • Зарегистрирован: 22.07.19
  • Сообщений: 4224
  • Уважение: +272
  • Позитив: +23
  • Пол: Мужской
  • Возраст: 47 [1977-09-08]
  • Провел на форуме:
    1 месяц 15 дней
  • Последний визит:
    15.10.24 19:48
  • Награды:
    31,31#(от Блонди),36#(от Блонди),49#(от Триатмы),59#(от Блонди),21#(от Григорий Р),9#(от Григорий Р),129#(от Артмеиды),109#(от Lisa),82#(от Бастет),61#(от Бастет)

Поэтому у меня возникает вопрос :

Каким образом у вас это пространство изменяется?

Тогда это уже другой термин.

Обозначающий под пространством всё то в чём находиться определенный объект.

Тогда это очень абстрактное понятие не имеющее четких координат.

Но может иметь тип формы.

Искривлённую, прямую, двух или трёх мерную.

Вывод: под одним словом скрыто в действительности два похожих термина.

Подпись автора

Всё ни так как кажется.
Спроси меня и я не отвечу тебе. Но расскажу новое и чудное, то что сам не знаю.

0

679

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p80065,Сергей написал(а):

Я их уже боюсь. Ну ладно, если один  Вова-🌻. Но этих чудиков уже трое

У них просто акция, вот Алис и ошакалилось: купи один - два в подарок!:D

0

680

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p80092,Ystyrgar написал(а):

Экватор, наконец.
Гриня, движение по экватору, это не отрезок АБ. Это окружность АА,

Наруби отрезки по линии экватора. Любые. И летай по ним. На проекции это будет прямые отрезки.

0

681

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80080,Блонди написал(а):

Дубинушка, это та же программа, что Вы использовали уже.

Flightradar.Дубинушка, ты показала зону радиусом километров в 100 вокруг аэропорта.Это глиссады

Наравне с дугообразными траекториями есть еще и прямые.
Почему?

На ом снимке  на который ты сослалась, вообще зона аэропррта. Что увидишь на расстоянии 100 км?

0

682

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p80094,Григорий Р написал(а):

Глупец, гравитация действует во всей плотности Земли. Не только во внешнем пространстве.
В очень глубокой шахте тоже. Вплоть до центра.
А ведь ты говлрил, что гравитация есть следствие искривления пространства.
Значит пространство кривое  и в толще шара.
Ты же не будешь стоять на том, что пространства там нет, оно вытеснено веществом.

Составляющие тЕла ровно также обладают свойством искривлять пространство, посему взаимодействуют между собой, представляя такое тело. Драмматургия в чем, маэстро?:D

0

683

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p80092,Ystyrgar написал(а):

В полной развертке у тебя любая параллель будет отнюдь не прямой, а явит собой окружность, как и экватор.

В полной развёртке, равнопромежуточной изоцилиндрике, которую используют в ЦУПе
параллели и меридианы параллельно перпендикулярны.

0

684

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80082,Григорий Р написал(а):

На плоской проекции это прямая!

Да иди ты в *афродиту*. Маршрут самолета летяшего по экватору так же будет дугой.Лечись, баран тупорылый

Отклонение от экватора даёт кривизну. Чем дальше тем круче из -за искажений проекции.

Херекции или эрекции. У тебя мозги рыпки гуппи.Ты начинаешь говорить о одном.заканчиваешь о другом. Или вообще вчсе в кучу валишь. Не, гриш, если ты неординарный человек, ты так и скажи

И это никак не доказывает искривление пространства.

Слышь, идиотина, Еще раз объясняю для  осеменителя-поверхность земли это свернутое в сферу двухмерное пространство.
Слушай,хряк производитель, ты таким тупым говорливым уродом стал из за того, что в христа уверовал, или уверовал в христа, потому что тупой хряк-производитель?

0

685

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p80101,Григорий Р написал(а):

Наруби отрезки по линии экватора. Любые. И летай по ним. На проекции это будет прямые отрезки.

Без поправки на время ты сядешь в болото, как раз километров за -дцать до ближайшей полосы.
Поправку на время компенсирует дуга, увеличивая (на деле же нормализуя) масштабированное расстояние.
Не рассказывай мне сказки, Гриня.

P.S. прямая развертка любых отрезков экватора даст тебе дуги, а целого - окружность, если што.
Можешь проверить.

0

686

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80086,Блонди написал(а):

Гриша, ты почитай, что по ссылке написано, которую Серёженька нам скидывал в доказательство искривления пространства - https://www.frequentflyers.ru/2014/04/0 … uting_faq/

Что называется - Серёжа смотрит в книгу и видит фигу.

Как же с *муськой* тяжело.Читает, почему на плоской карте дуга, не может понять и путает  поверхность с пространством-временем. Ну тупая , че

0

687

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80087,Блонди написал(а):

"Просто дисплеи плоские, а Земля круглая, и проекция объемной карты на плоскую видоизменяет ее пропорции: чем ближе к полюсам, тем более изогнутой окажется «дуга»."

Ну наконец то, тупая идиотка после трех недель разговора   нашла нужную цитату  которую ей пытались в тупую башку вколотить три недели. Аплодисменты   идиотке.Осталось только, что бы тупая ссаная дырка во первых поняла, что это значит.
Тебе, в тупую башку вколачивали, что это перенос из искривленного пространства на плоскую двухмерную поверхность.Почему искривленного? Потому что поверхность шара-искривленное двухмерное пространство

И во вторых  залезла в учебники геометрии и начала учить, что же такое пространство и почему говорят о искривлении когда  плоскость заворачивается в шар.
Но наверное не дождемся

Отредактировано Сергей (22.01.20 15:20)

0

688

  • Автор: Ystyrgar
  • Ветеран
  • Зарегистрирован: 02.08.19
  • Сообщений: 4408
  • Уважение: +641
  • Позитив: +477
  • Провел на форуме:
    1 месяц 5 дней
  • Последний визит:
    22.09.20 08:26
  • Награды:
    31,12#(от Артемиды),18#(от Артемиды),5#(от Григория Р),6#(от Блонди),3#(от Блонди),63#(от Блонди),64#(от Блонди),35#(от Григория Р),71#(от Димы1972),52#(от Владимира),81#(от Блонди и Григория Р),50#(от~Татьяна~),34#(от~Татьяна~)
#p80106,Григорий Р написал(а):

В полной развёртке, равнопромежуточной изоцилиндрике, которую используют в ЦУПе
параллели и меридианы параллельно перпендикулярны.

Мы говорим о СФЕРЕ, а не о схемах, ей приближенных, Гриня. На карте, без учета объема, параллели и меридианы тоже строго прямые и перпендикулярны друг другу. Только вот соотношения частей суши там отображено с большим искажением. Не знал?
А про цилиндр я тебе расписал подробно выше, зря ты не читал.

0

689

  • Автор: Сергей
  • Ветеран
  • Зарегистрирован: 30.07.19
  • Сообщений: 12193
  • Уважение: +1504
  • Позитив: +738
  • Провел на форуме:
    1 месяц 27 дней
  • Последний визит:
    08.03.22 19:49
  • Награды:
    31,12#(от Артемиды),16#(от Артемиды),22#(от Блонди и Григория Р),21#(от Блонди),18#(от ~Татьяны~),4#(от Григория Р),24#(от Григория Р),47#(от Блонди),52#(от Триатмы),63#(от Блонди),35#(от Григория Р),65#(от Блонди),67#(от Триатмы),70#(от Димы1972),73#(от Блонди),74#(от Блонди Димы1972 и Григория Р),75#(от Григория Р),76#(от Григория Р),77#(от air),78#(от Димы1972),66#(от Владимира),68#(от Владимира),31#(от Димы1972),81#(от Блонди и Григория Р),83#(от Dima и Григория Р),81#(от Артемиды)
#p80088,Григорий Р написал(а):

Да, Сереженька по глупости начал пихать эти картинки, подсмотренные в Шереметьего из-за плеча дипломированных диспетчеров. Пока со шлангом бегал и воду включал.

Сейчас апельсины суёт.  Если всё это задумывалось, чтобы показать нам, что земля круглая, и путешественник делает круг по поверхности, то достаточно апельсина.
Он нам хотел какое-то свое открытие показать.
Но вовремя спрыгнул.
Ну, как вовремя. На тысячной странице где-то.

Отредактировано Григорий Р (Сегодня 11:11)

#p80088,Григорий Р написал(а):

Да, Сереженька по глупости начал пихать эти картинки, подсмотренные в Шереметьего из-за плеча дипломированных диспетчеров. Пока со шлангом бегал и воду включал.

Сейчас апельсины суёт.  Если всё это задумывалось, чтобы показать нам, что земля круглая, и путешественник делает круг по поверхности, то достаточно апельсина.
Он нам хотел какое-то свое открытие показать.
Но вовремя спрыгнул.
Ну, как вовремя. На тысячной странице где-то.

Отредактировано Григорий Р (Сегодня 11:11)

То есть, ты даже не понял о чем тебе тут втолковывали все три недели? Ну не удивлен.  Бестолку. Умный в христиане не пойдет, а тратить на  шприц для спермы еще три недели своего времени объясняя геометрию, нет никакого желания

0

690

  • Автор: Григорий Р
  • Ветеран
  • Григорий Р
  • Зарегистрирован: 23.01.19
  • Сообщений: 16730
  • Уважение: +4656
  • Позитив: +5034
  • Провел на форуме:
    5 месяцев 4 дня
  • Последний визит:
    Сегодня 04:49
  • Награды:
    31,20#(от Артемиды),10#(от Блонди),13#(от ~Татьяны~),39#(от Блонди),16#(от Артемиды),58#(от Блонди),72#(от Сергея),80,16#(от Enigma),85#(от Блонди),12#(от Admin),97#(от Enigma),98#(от Enigma),103#(от Enigma),10#(от Стефании),26#(от Стефании),27#(от Стефании),97#(от Стефании),118#(от Ильи),117#(от Духовного Гуру)),139#(от Dima),10#(от Бастет)
#p80086,Блонди написал(а):

Гриша, ты почитай, что по ссылке написано, которую Серёженька нам скидывал в доказательство искривления пространства - https://www.frequentflyers.ru/2014/04/0 … uting_faq/

Что называется - Серёжа смотрит в книгу и видит фигу.

Деменция.

0

Страница:   1 … 21 22 23 24 25 … 34  

Вы здесь » Межрелигиозный форум » Что нового в мире науки? » Пространство